\bld2{Reachability based (Ri)sk Aware (P)lanner.}
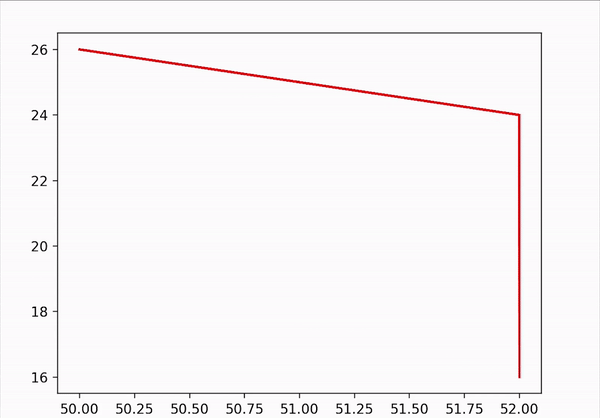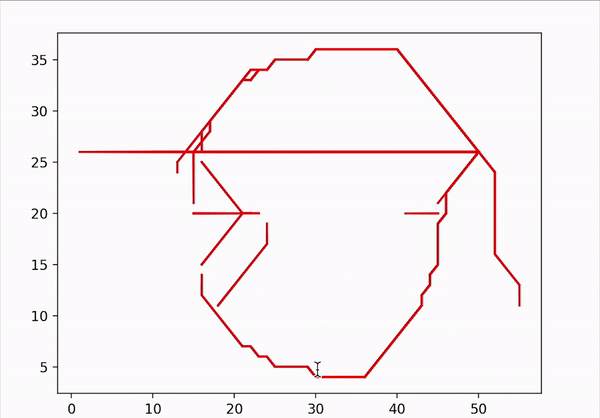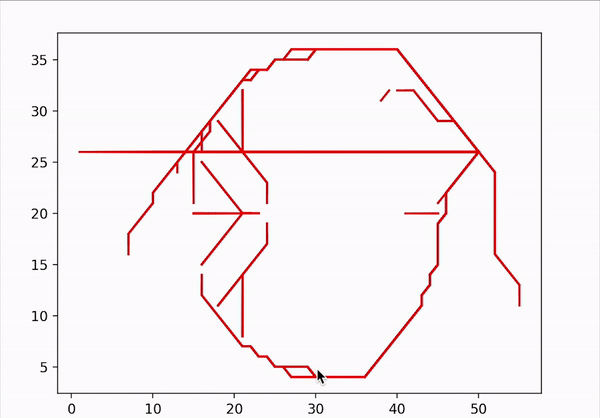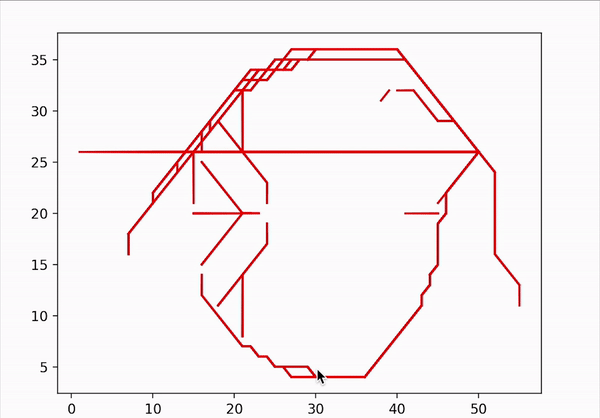
RiP is a reachability based behavioural planner that prioritizes certain behaviour over the other. In this case, the priority order being:
- No interaction with the “Danger” zone
- Total length of the trajectory<constant (100)
- Minimize the time spent in “Risk” zone
- Minimize the total path length
(This order of the can be rearranged to get different results.)
The risk is minimized by assigining risk boundaries around the obstacles and then optimizing the path for length as well as risk. This algorithm is most suited for cases where the obstacles are adverserial and missions where safety is of utmost priority.
Theoretical Framework
Reachability Analysis
The core of our approach lies in computing reachable sets, which represent all possible states that can be reached by the system under given constraints. For a dynamical system:
$\dot{x} = f(x, u)$
where $x \in \mathbb{R}^n$ is the state vector and $u \in \mathcal{U}$ is the control input, the reachable set $\mathcal{R}(t)$ at time $t$ is defined as:
\[\mathcal{R}(t) = {x(t) | x(0) \in \mathcal{X}_0, u(\tau) \in \mathcal{U}, \tau \in [0,t]}\]where $\mathcal{X}_0$ is the set of initial states.
Risk-Aware Planning
The risk assessment is formulated through a multi-objective optimization problem:
$\min_{u \in \mathcal{U}} \left[ \int_0^T \ell(x(t), u(t)) dt + \lambda \int_0^T \rho(x(t)) dt \right]$
where:
- $\ell(x,u)$ is the path cost function
- $\rho(x)$ is the risk function
- $\lambda$ is the risk aversion parameter
- $T$ is the planning horizon
The risk function $\rho(x)$ is defined as:
\[\rho(x) = \sum_{i=1}^{N} w_i \exp\left(-\frac{|x - x_i|^2}{2\sigma_i^2}\right)\]where:
- $x_i$ represents the center of the $i$-th obstacle
- $\sigma_i$ is the risk spread parameter
- $w_i$ is the weight associated with each obstacle
Safety Guarantees
The safety constraints are enforced through a barrier function approach:
\[B(x) = \min_{i} \left( |x - x_i| - r_i \right)\]where $r_i$ is the safety radius of the $i$-th obstacle. The planner ensures:
$B(x(t)) \geq 0, \forall t \in [0,T]$
Optimization Formulation
The complete optimization problem can be written as:
$\begin{aligned} \min_{u \in \mathcal{U}} & \int_0^T \ell(x(t), u(t)) dt + \lambda \int_0^T \rho(x(t)) dt
\text{subject to} & \dot{x} = f(x, u)
& B(x(t)) \geq 0, \forall t \in [0,T]
& x(0) \in \mathcal{X}_0
& x(T) \in \mathcal{X}_f \end{aligned}$
where $\mathcal{X}_f$ is the set of goal states.
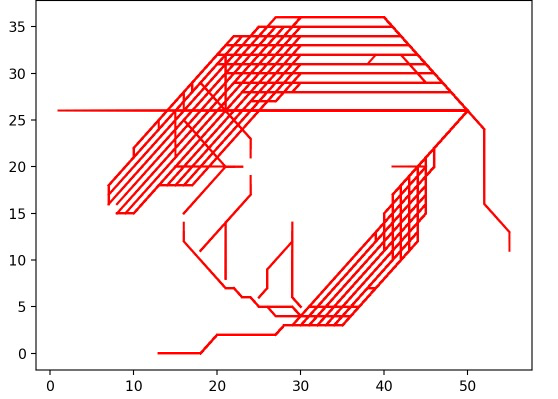
All possible explored paths
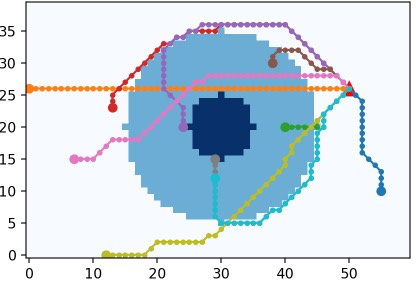
Final chosen path
Code repository : Feel free to browse and access our software stack: RiP-Planner
More on the project and its documentation is in works. Coming soon!