\bld2{Meta QLearning experiments to optimize robot walking patterns.}
Implemented Meta-Q-Learning for optimizing humanoid walking patterns. The project also demonstrate its effectiveness in improving stability, efficiency, and adaptability. Additionally, this work also explores the transferability of Meta-Q-Learning to new tasks with minimal tuning.
Conducted experiments: Test how adaptable the humanoid is by performing:
- Side stepping
- Ascending and Descending
Theoretical Framework
Meta-Learning in Reinforcement Learning
Meta-learning, or “learning to learn,” is particularly powerful in reinforcement learning scenarios where we want an agent to quickly adapt to new tasks. In the context of humanoid robotics, this means learning a policy that can rapidly adapt to different walking patterns, terrains, and disturbances.
The Meta Q-Learning approach we implemented combines several key concepts:
- Task Distribution :
- We define a distribution of tasks (different walking patterns, terrains, and disturbances)
- Each task represents a different MDP (Markov Decision Process) with shared structure
- The agent learns to quickly adapt to new tasks from this distribution
- Meta-Policy Architecture :
- The meta-policy consists of two components:
- A task-agnostic base policy that captures common walking patterns
- A task-specific adaptation mechanism that modifies the base policy for new tasks
- This architecture enables rapid adaptation to new scenarios
- The meta-policy consists of two components:
- Optimization Objective : The meta-learning objective can be expressed as:
$\min_{\theta} \mathbb{E}_{T \sim p(T)}[L_T(\theta)]$
where:
* $\theta$ represents the meta-parameters
* $p(T)$ is the task distribution
* $L_T$ is the loss function for task T
Implementation Details
- State Space :
- Joint angles and velocities
- Center of mass position and velocity
- Contact forces
- Task-specific features (terrain height, disturbance magnitude)
- Action Space :
- Joint torques
- Desired joint positions
- Balance control parameters
- Reward Function : The reward function combines multiple objectives:
$R = w_1R_{\text{stability}} + w_2R_{\text{energy}} + w_3R_{\text{task}}$
where:
* $R_{\text{stability}}$: Penalizes deviations from stable walking
* $R_{\text{energy}}$: Encourages energy-efficient movements
* $R_{\text{task}}$: Rewards task-specific objectives 4. **Meta-Learning Algorithm** : We use a variant of Model-Agnostic Meta-Learning (MAML) adapted for Q-learning:
* Inner loop: Task-specific adaptation using Q-learning
* Outer loop: Meta-parameter updates using gradient descent
* The adaptation process can be expressed as:
$\theta’ = \theta - \alpha\nabla_{\theta}L_T(\theta)$
where $\alpha$ is the adaptation rate
Transfer Learning Mechanism
The key to successful transfer learning in our implementation is the hierarchical structure of the policy:
- Base Policy Layer :
- Learns fundamental walking patterns
- Captures common dynamics across tasks
- Provides a stable starting point for adaptation
- Adaptation Layer :
- Modifies the base policy for specific tasks
- Uses task-specific features to guide adaptation
- Enables rapid learning of new behaviors
This hierarchical structure allows the agent to:
- Maintain stable walking patterns while adapting to new tasks
- Transfer knowledge between similar tasks
- Learn new tasks with minimal data
Inference
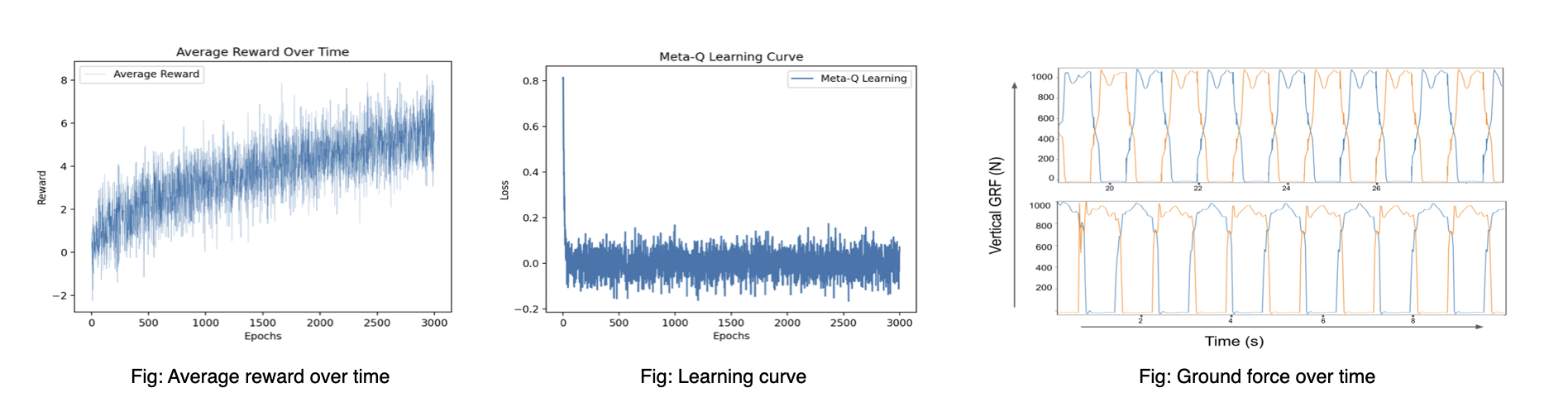
This work was done as a fun project to learn RL and its applications, so I have not drawn a lot of theoretical inferences. That being said, here are some quantitative inferences from the work: 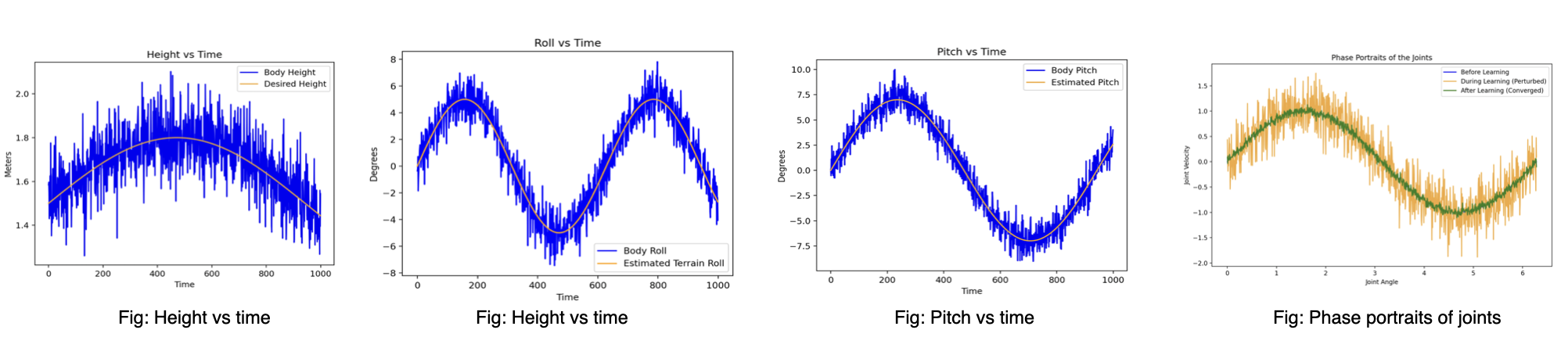
Code repository : Feel free to browse and access the software stack: https://github.com/gokulp01/meta-qlearning-humanoid