Extraterrestrial multi-robot planner.
Multi-robot teams have been used for a variety of navigation and mapping applications. They have proven to provide better time efficacy and output than using a singular robot in doing the same. A place where such an implementation may have a lot of potential is in the exploration of planets and other similar terrestrial bodies, which is what this study aims to focus on. With space research thriving more than ever, a decentralized multi-robot system has the potential to deliver results many more times than a single ground robot would.
Theoretical Framework
Multi-Robot Coordination
For a team of $n$ robots, each robot $i$ has a state vector $x_i \in \mathbb{R}^d$ and control input $u_i \in \mathcal{U}_i$. The collective state space is:
$\mathcal{X} = \prod_{i=1}^n \mathbb{R}^d$
The decentralized control law for each robot is given by:
$\dot{x}i = f_i(x_i, u_i) + \sum{ {j \in \mathcal{N}i} } g{ij}(x_i,x_j)$
where:
- $f_i$ represents the individual robot dynamics
- $g_{ij}$ represents the interaction dynamics between robots $i$ and $j$
- $\mathcal{N}_i$ is the set of neighboring robots
Space-Filling Optimization
The space-filling problem is formulated as a coverage optimization:
| $\min_{X} \sum_{i=1}^n \int_{\mathcal{W}} \min_{j} | x - x_j | ^2 dx$ |
where:
- $X = {x_1, …, x_n}$ is the set of robot positions
- $\mathcal{W}$ is the workspace
- The objective minimizes the maximum distance from any point to its nearest robot
Collision Avoidance
To ensure no path overlap, we implement a potential field-based approach:
$U_{ij}(x_i, x_j) = \begin{cases} \frac{1}{2}\eta\left(\frac{1}{|x_i - x_j|} - \frac{1}{d_0}\right)^2 & \text{if } |x_i - x_j| \leq d_0
0 & \text{otherwise} \end{cases}$
where:
- $\eta$ is the repulsion strength
- $d_0$ is the minimum safe distance
The total potential field for robot $i$ is:
$U_i(x_i) = \sum_{j \in \mathcal{N}i} U{ij}(x_i, x_j)$
Decentralized Control Law
The final control law for each robot combines coverage optimization and collision avoidance:
| $u_i = -\nabla_{x_i} \left( \int_{\mathcal{W}} \min_{j} | x - x_j | ^2 dx + U_i(x_i) \right)$ |
This ensures:
- Optimal space coverage
- Collision-free navigation
- Decentralized operation
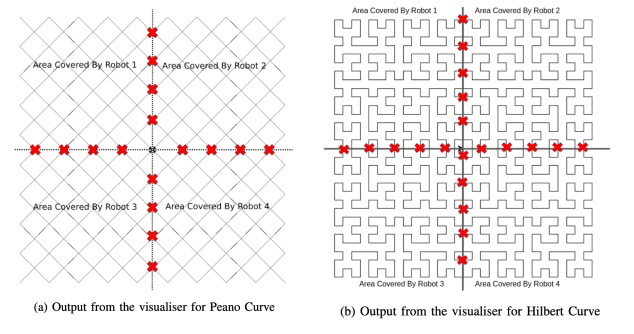
This paper introduces an optimized space-filling technique and tries to achieve autonomous multi-robot navigation without any path overlap.
Code repository and Report:
- Software stack: https://github.com/raghavthakar/kobu
- Publications, Report: https://github.com/raghavthakar/kobu/blob/main/kobu.pdf
- Watch it in action here: https://www.youtube.com/watch?v=NxmvM7g0AX4